2. Representing Numbers as Points on a
Number Line

Notes:

Thinking of numbers as points along a number line can help us understand arithmetic properties that involve zero, negative numbers, inequalities, and distances. Here’s the real number line:

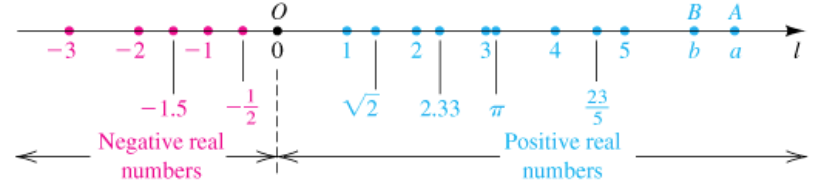
• We go from negative numbers on the left to positive numbers on the right, with 0 in between.
• We can place points to represent integers, such as −3 and 3, rational numbers, such as −1/2 and 1/3, and irrational numbers, such as √2 and π.
• The points labeled A and B have associated numbers a and b that represent coordinates.

Sign rules

• Consider multiplying two numbers, a x b. If a and b have the same sign, then the product ab is positive. If a and b have opposite signs, then ab is negative.
• Similarly, if we divide two numbers, a ÷ b. If a and b have the same sign, then the quotient a/b is positive. If a and b have opposite signs, then a/b is negative.

Properties of negatives

• If we multiply a number a by −1 we get −a: (−1)a = −a. For example, (−1)(3) = −3.
• If we take the negative of a negative number, we get the original number again: −(−3) = 3. For example, −(−3) = 3.
• If we multiply −a by b or a by −b we get the same answer: (−a)b = a(−b) = −(ab). For example, (−3)4 = 3(−4) = −(3×4) = −12.
• But if we multiply −a by −b we get (−a)(−b) = ab. For example, (−3)(−4) = 12

Properties of zero

• If we multiply a number a by 0 we get 0: 3 × 0 = 0. For example, 3 × 0 = 0.
• If ab = 0 then a = 0 or b = 0 (or both a = b = 0). This is called the zero-factor theorem, and it comes up a lot when solving equations

Connection between subtraction and addition

• One way to subtract b from a is to add −b to a: a − b = a + (−b). For example, 3 − 4 = 3 +(−4) = −1 and 3 − (−4) = 3 + 4 = 7.

Inequalities

• First, strict inequalities: a > b if a − b is positive and 3 < 4 if 3 − 4 is negative. For example, 3 < 4 because 3 − 4 = −1 and 3 > −4 because 3 − (−4) = 7.
• • If we have two numbers a and b, either a > b, a < b, or a = b.
• Next, nonstrict inequalities: a ≥ b if a > b or a = b and a ≤ b if a < b or a = b.

Absolute values

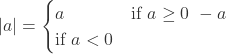
• For example, |3| = 3 and | − 4| = 4. Think of the absolute value as representing the magnitude of a number without regard to its sign.
• This leads to the notion of the distance between two numbers: d(a,b) = |b − a| = |a − b|. For example, d(3,4) = |3 − 4| = | − 1| = 1, d(3, −4) = |3 − (−4)| = |7| = 7