13. Multiplying and Dividing Rational Expressions

Photo Of Person Teaching On White Board by Vanessa Garcia is used under the pexels license.

Learning Objective:

Multiply rational expressions by multiplying the numerators and multiplying the denominators. Use the connection between division and multiplying by the reciprocal to divide rational expressions. Apply factoring, if possible, to simplify a rational expression before multiplying or dividing.

Video:
Interactive Activity

PDF Notes Link:

Multiplying Dividing Rational ExpressionsDownload

Notes:

Multiplying rational expressions

To multiply two fractions, we simply multiply the numerators and multiply the denominators. For example,

\frac{2}{3} \times \frac{5}{7} = \frac{2 \times 5}{3 \times 7} = \frac{10}{21}

We do the same thing when multiplying rational expressions. For example,

\frac{2x^{2}+3}{-3x+1} \times \frac{x-4}{x^{2}+2} = \frac{(2x^{2}+3)(x-4)}{(-3x+1)(x^{2}+2)} = \frac{2x^{3}-8x^{2}+3x-12}{-3x^{3}+x^{2}-6x+2}

The resulting rational expression is not defined when x = −1/3 and cannot be simplified

Dividing rational expressions

To divide a fraction, a/b, by another fraction, c/d, we multiply a/b by the reciprocal of c/d, i.e., d/c.

For example,

\frac{2}{3} \div \frac{5}{7} = \frac{2}{3} \times \frac{7}{5} = \frac{2 \times 7}{3 \times 5} = \frac{14}{15}

We do the same thing when dividing rational expressions.

For example,

\frac{2x^{2}+3}{-3x+1} \div \frac{x-4}{x^{2}+2} = \frac{2x^{2}+3}{-3x+1} \times \frac{x^{2}+2}{x-4} = \frac{2x^{4}+7x^{2}+6}{-3x^{2}+13x-4}

The resulting rational expression is not defined when x = -1/3 or x = 4 and cannot be simplified.

Simplifying using factoring

It’s nice if the rational expressions we end up with can be simplified. It’s generally easier to do this if we can factor any of the polynomials before multiplying. For example,

\frac{x^{2}+x-6}{x-1}\times\frac{x^{2}-2x+1}{x^{2}-4}=\frac{x^{4}-x^{3}-7x^{2}+13x-6}{x^{3}-x^{2}-4x+4}, \quad \{\forall x \neq -2, 1, 2\}.

This is not particularly easy to simplify from here.

However, if we factor the numerators and denominators of the original rational expressions before multiplying, we get a much simpler answer:

More Examples

\frac{x^{2}}{x^{2}-6x+9}\div\frac{4x}{2x-6}=\frac{x^{2}}{x^{2}-6x+9}\times\frac{2x-6}{4x}=\frac{x^{2}}{(x-3)^{2}}\times\frac{2(x-3)}{4x}=\frac{x}{2(x-3)},\{\forall x\ne0,3\}.

\frac{x^{2}-x-6}{x^{3}+2x^{2}}\times\frac{x^{2}+2x+1}{2x^{2}-4x-6}=\frac{(x+2)(x-3)}{x^{2}(x+2)}\times\frac{(x+1)^{2}}{2(x-3)(x+1)}=\frac{x+1}{2x^{2}},\{\forall x\ne-2,-1,0,3\}.

\frac{x^{3}+3x^{2}+3x+9}{x^{2}-4}\div\frac{x^{2}+2x-3}{x^{2}+x-2}=\frac{(x^{2}+3)(x+3)}{(x+2)(x-2)}\times\frac{(x+2)(x-1)}{(x+3)(x-1)}=\frac{x^{2}+3}{x-2},\{\forall x\ne-3,-2,1,2\}.

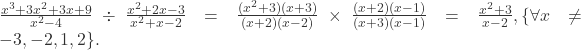
Transcript:

The video transcripts are accessible for viewing and downloading below.

Multiplying-and-Dividing-Rational-ExpressionsDownload

Video Link:

https://media.tru.ca/media/Math+13/0_vv1mus6g

Print Friendly, PDF & Email

Similar Posts